A meta-model, or surrogate model, is a close and fast approximation to an original model whose computational cost is usually very high. When inputs or outputs of the original model are high-dimensional, dimension reduction is part of the meta-model design. The reduced model is then replaced using learning, statistical or interpolation methods, e.g. using Gaussian process regression or radial basis functions.
Below is an example with an urban noise simulation, which is carried out with a noise mapping model taking traffic data as inputs. On the right, the meta-model generates a very similar noise map, but with a speed-up factor of 25,000.
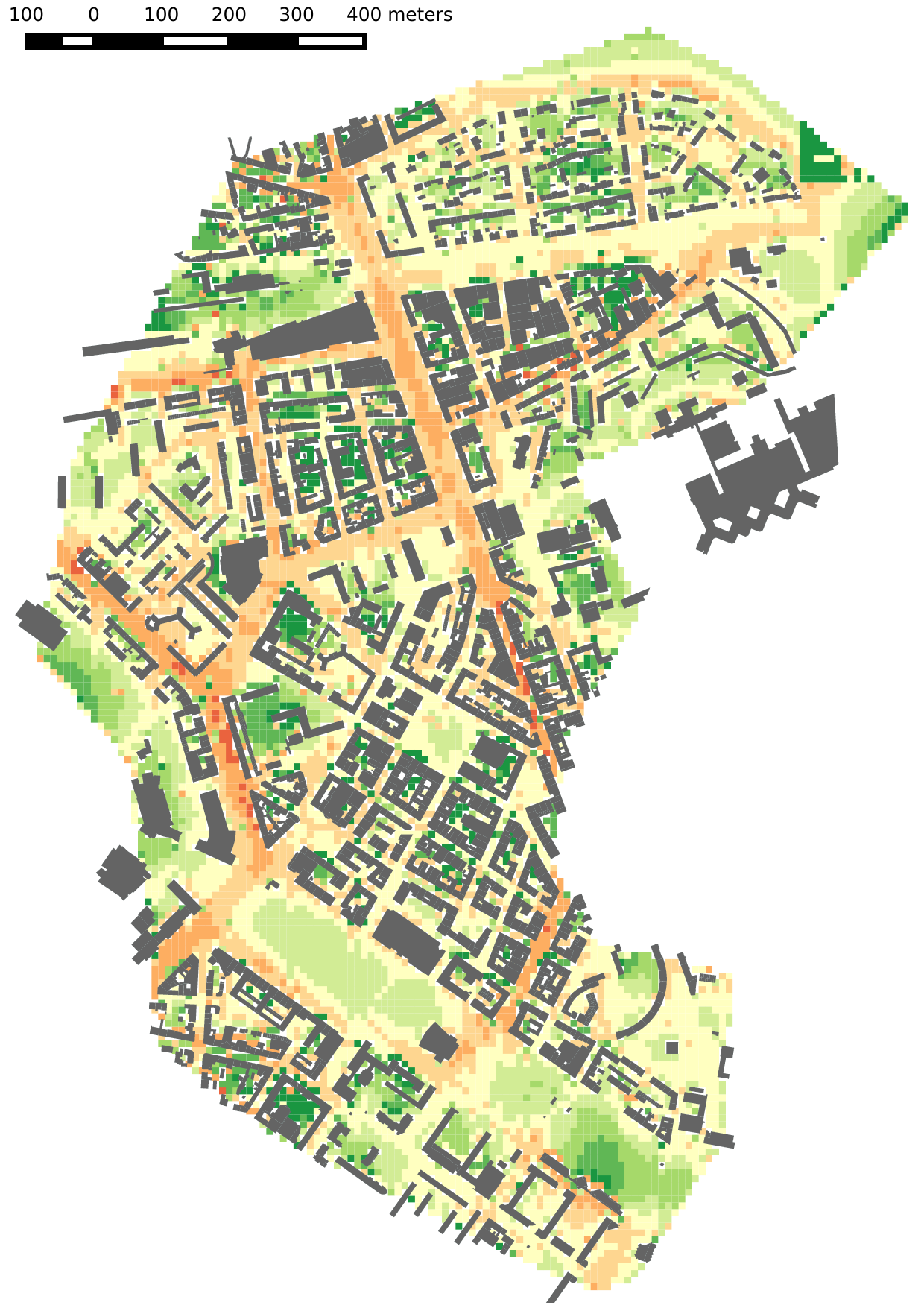
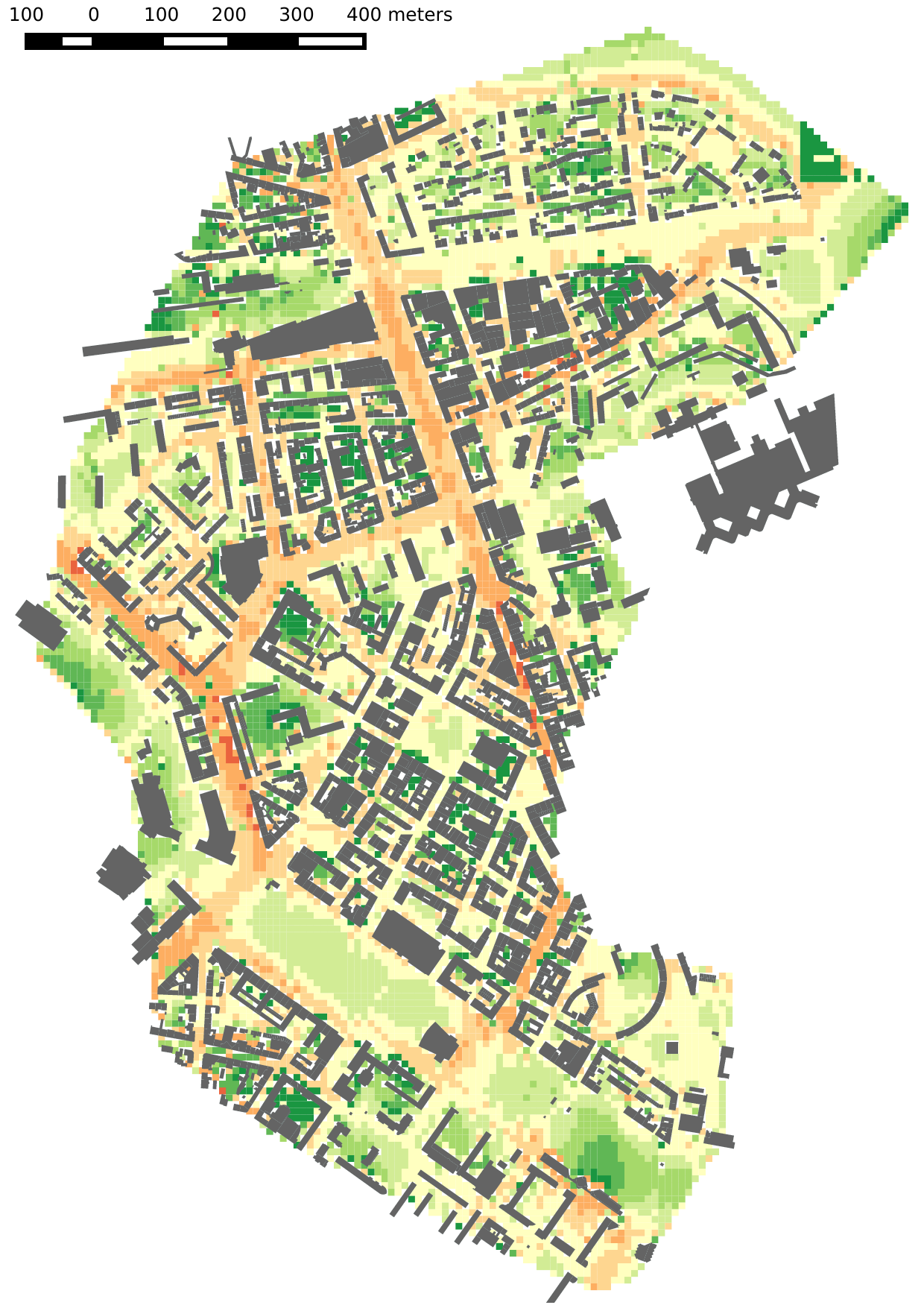
On the right, the meta-model simulation computed in 0.065 second.
Another example is provided below for air pollution (NO2 concentrations) with a video that shows how fast a new map can be computed, whereas the original model would required 15 minutes to an hour of computations for each new map.